En matemáticas, una ecuación es una igualdadnota 1 entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos oincógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes o constantes; y también variables cuya magnitud se haya establecido como resultado de otras operaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:
la variable  representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen ambos miembros; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables la hacen cierta.
representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen ambos miembros; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables la hacen cierta.
 representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen ambos miembros; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables la hacen cierta.
representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen ambos miembros; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables la hacen cierta.
Se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisfaga. Para el caso dado, la solución es:
Resolver una ecuación es encontrar su dominio solución, que es el conjunto de valores de las incógnitas para los cuales la igualdad se cumple. Todo problema matemático puede expresarse en forma de una o más ecuaciones; sin embargo no todas las ecuaciones tienen solución, ya que es posible que no exista ningún valor de la incógnita que haga cierta una igualdad dada. En ese caso, el conjunto de soluciones de la ecuación será vacío y se dice que la ecuación no es resoluble. De igual modo, puede tener un único valor, o varios, o incluso infinitos valores, siendo cada uno de ellos una solución particular de la ecuación. Si cualquier valor de la incógnita hace cumplir la igualdad (esto es, no existe ningún valor para el cual no se cumpla) la expresión se llama identidad.
De manera más general, una ecuación tendrá la forma
donde F, G son operadores y a, b pueden ser valores numéricos, variables o funciones (en este último caso se tiene una ecuación funcional). Por ejemplo, la ecuación real (donde las incógnitas están sobre los números reales):
tiene por soluciones o raíces el conjunto infinito de valores

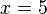




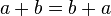

 , que es igual a sumar un
, que es igual a sumar un 

 ó
ó 


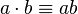
 , que es igual a multiplicar por el
, que es igual a multiplicar por el 



 (n veces)
(n veces) y
y 
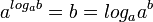
![\ a^{m/n} \equiv (\sqrt[n]{a^{m}})](http://upload.wikimedia.org/math/9/d/c/9dce189c9cd5c2644b62a96c54e7eb83.png) y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver:
y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver: 

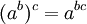

 entonces
entonces 
 entonces
entonces 
 entonces
entonces  y
y 

 y
y  no es cero, entonces
no es cero, entonces  y
y  entonces
entonces 
 entonces
entonces 
 entonces
entonces 
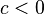 entonces
entonces 
